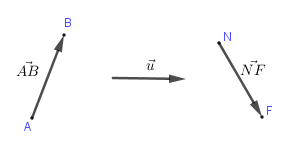
Vectơ là đoạn thẳng có hướng, nghĩa là trong hai điểm mút của đoạn thẳng đã chỉ rõ điểm nào là điểm đầu, điểm nào là điểm cuối.
Đang xem: Vectơ là gì, véctơ có những Đặc Điểm tính chất nào? véctơ có những Đặc Điểm tính chất nào
Vectơ có điểm đầu là $A,$ điểm cuối là $B$ ta kí hiệu $overrightarrow {AB} $
Vectơ còn được kí hiệu là: $overrightarrow a ,{
m{ }}overrightarrow b ,{
m{ }}overrightarrow x ,{
m{ }}overrightarrow y ,…$
Vectơ – không là vectơ có điểm đầu trùng điểm cuối. Kí hiệu là (overrightarrow 0 )
2. Hai vectơ cùng phương, cùng hướng
– Đường thẳng đi qua điểm đầu và điểm cuối của vectơ gọi là giá của vectơ
– Hai vectơ có giá song song hoặc trùng nhau gọi là hai vectơ cùng phương
– Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng.
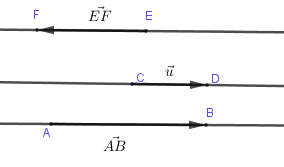
Ví dụ: Ở hình vẽ trên trên thì hai vectơ (overrightarrow {AB} ) và (overrightarrow {CD} ) cùng hướng còn (overrightarrow {EF} ) và (overrightarrow {CD} ) ngược hướng.
Đặc biệt: vectơ – không cùng hướng với mọi véc tơ.
3. Hai vectơ bằng nhau
– Độ dài đoạn thẳng $AB$ gọi là độ dài véc tơ $overrightarrow {AB} $, kí hiệu $left| {overrightarrow {AB} }
ight|$.
Vậy $left| {overrightarrow {AB} }
ight| = AB$
– Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài.
Xem thêm: Nhạc Vina House Là Gì ? Quẩy Vinahey Như Thế Nào Mới “Chất”?
– Hai vecto đối nhau nếu chúng ngược hướng và cùng độ dài.
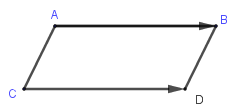
Ví dụ: Cho hình bình hành (ABDC) khi đó:
(overrightarrow {AB} = overrightarrow {CD} ) vì chúng cùng hướng và cùng độ dài.
(overrightarrow {AB} )và (overrightarrow {DC} ) là hai véc tơ đối nhau vì chúng ngược hướng và cùng độ dài.
Chứng minh:

Phản chứng:
Giả sử có điểm (M) sao cho (overrightarrow {MA} = overrightarrow {MB} )
Khi đó (overrightarrow {MA} ,overrightarrow {MB} ) cùng hướng và cùng độ dài.
Xem thêm: Trượt Giá Là Gì ? Làm Sao Để Tránh Trượt Giá Khi Giao Dịch Forex
Vì (overrightarrow {MA} ,overrightarrow {MB} ) cùng hướng nên (M) chỉ nằm trên đường thẳng (AB) và nằm ngoài hai điểm (A,B)
Như vậy thì chỉ xảy ra (MA MB) nên mâu thuẫn với giả thiết cùng độ dài.
Do đó không tồn tại điểm (M) thỏa mãn (overrightarrow {MA} = overrightarrow {MB} )
Tuy nhiên, nếu (A,B) trùng nhau thì ta lại có vô số điểm (M) thỏa mãn (overrightarrow {MA} = overrightarrow {MB} )
Mục lục – Toán 10
CHƯƠNG 1: MỆNH ĐỀ, TẬP HỢP
Bài 1: Mệnh đề
Bài 2: Mệnh đề chứa biến và áp dụng vào suy luận toán học
Bài 3: Tập hợp
Bài 4: Các phép toán trên tập hợp
Bài 5: Các tập hợp số
Bài 6: Ôn tập chương I
CHƯƠNG 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI
Bài 1: Đại cương về hàm số
Bài 2: Hàm số bậc nhất
Bài 3: Hàm số bậc hai
Bài 4: Một số bài toán về đồ thị hàm số bậc nhất
Bài 5: Phương pháp giải các bài toán về hàm số bậc hai
Bài 6: Ôn tập chương 2
CHƯƠNG 3: PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH
Bài 1: Đại cương về phương trình
Bài 2: Phương trình bậc nhất và bậc hai một ẩn
Bài 3: Phương pháp giải phương trình bậc ba, bậc bốn đặc biệt
Bài 4: Phương trình chứa dấu giá trị tuyệt đối
Bài 5: Phương trình chứa căn
Bài 6: Hệ hai phương trình bậc nhất hai ẩn
Bài 7: Hệ phương trình có cấu trúc đặc biệt
CHƯƠNG 4: BẤT ĐẲNG THỨC, BẤT PHƯƠNG TRÌNH
Bài 1: Bất đẳng thức
Bài 2: Đại cương về bất phương trình
Bài 3: Bất phương trình và hệ bất phương trình bậc nhất một ẩn
Bài 4: Dấu của nhị thức bậc nhất
Bài 5: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
Bài 6: Dấu của tam thức bậc hai
Bài 7: Bất phương trình bậc hai
CHƯƠNG 5: THỐNG KÊ
Bài 1: Phương sai và độ lệch chuẩn
CHƯƠNG 6: GÓC LƯỢNG GIÁC VÀ CÔNG THỨC LƯỢNG GIÁC
Bài 1: Đơn vị đo góc và cung tròn, độ dài cung tròn
Bài 2: Góc lượng giác và cung lượng giác
Bài 3: Giá trị lượng giác của một góc (cung) lượng giác
Bài 4: Giá trị lượng giác của các góc có liên quan đặc biệt
Bài 5: Một số công thức biến đổi lượng giác
CHƯƠNG 7: VÉC TƠ
Bài 1: Các định nghĩa về véc tơ
Bài 2: Tổng của hai véc tơ
Bài 3: Hiệu của hai véc tơ
Bài 4: Tích của một véc tơ với một số
Bài 5: Hệ trục tọa độ trong mặt phẳng
Bài 6: Biểu thức tọa độ của các phép toán véc tơ
Bài 7: Ôn tập chương Véc tơ
CHƯƠNG 8: TÍCH VÔ HƯỚNG CỦA HAI VÉC TƠ VÀ ỨNG DỤNG
Bài 1: Giá trị lượng giác của một góc bất kì từ 0 đến 180 độ
Bài 2: Tích vô hướng của hai véc tơ
Bài 3: Biểu thức tọa độ của tích vô hướng
Bài 4: Hệ thức lượng trong tam giác
CHƯƠNG 9: PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
Bài 1: Một số khái niệm phương trình đường thẳng
Bài 2: Một số bài toán viết phương trình đường thẳng
Bài 3: Khoảng cách và góc
Bài 4: Phương trình đường tròn
Bài 5: Vị trí tương đối của đường thẳng với đường tròn
Bài 6: Elip
Bài 7: Hypebol

Học toán trực tuyến, tìm kiếm tài liệu toán và chia sẻ kiến thức toán học.
gocnhintangphat.com
Theo dõi chúng tôi trên