Bài học hôm nay gocnhintangphat.com xin giới thiệu tới các bạn khái niệm về trực tâm và các tính chất quan trọng trong tam giác. Để hiểu rõ hơn về chủ đề hôm nay mờibạn cùng tham khảo bài học dưới đây!
I. Lý thuyết về trực tâm của tam giác
1. Trực tâmlà gì?
Bađường xuất phát từ 3 đỉnh của tam giác và vuông góc vs cạnh đối diện sẽ giao nhau tại 1 điểm gọi là TT. Vì vậy giao điểm của ba đường cao trong tam giác chính là trực tâm của tam giác.
Đang xem: Tính chất trực tâm là gì, lý thuyết trực tâm của tam giác tính chất trực tâm, Đường cao tam giác
+ Đối với tam giác nhọn: Trực tâm nằm ở miền trong tam giác đó+ Đối với tam giác vuông: Trực tâm chình là đỉnh góc vuông+ Đối với tam giác tù: Trực tâm nằm ở miền ngoài tam giác đó
Công thức liên quan:
2. Tính chấtcủa trực tâm
Khoảng cách từ tâm đường tròn ngoại tiếp tam giác đó đến trung điểm cạnh nối hai đỉnh còn lại bằng 1/2 khoảng cách từ một đỉnh tới TT. Trực tâmtam giác vuông chính là đỉnh góc vuông của tam giác vuông đó. Nếu tam giác đã cho là tam giác cân thì đường cao cũng đồng thời là đường trung tuyến, đường phân giác và đường trung trực của đỉnh tam giác cân đó. Trong tam giác đều, trực tâm cũng đồng thời là trọng tâm, tâm đường tròn nội tiếp và ngoại tiếp của tam giác đó. Định lý Carnot:Đường cao tam giác ứng với một đỉnh cắtđường tròn ngoại tiếptại điểm thứ hai làđối xứngcủa TT qua cạnh tương ứng.
II. Bài tập về trực tâm tam giác
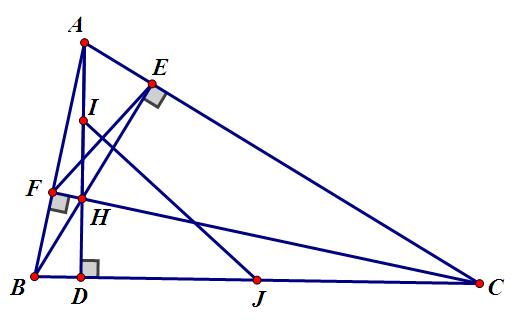
Bài tập: Cho△ABC có các đường cao AD;BE;CF cắt nhau tại H. I; J lần lượt là trung điểm của AH và BC.
a) Chứng minh:(JT⊥EF)
b) Chứng minh: (IE⊥JE)
c) Chứng minh: DA là tia phân giác của góc EDF.
d) Gọi P;Q là hai điểm đối xứng của D qua AB và AC
Chứng minh: P;F;E;Q thẳng hàng.
Xem thêm: Thuốc Tanakan Là Thuốc Gì ? Công Dụng & Liều Dùng Hello Bacsi
Lời giải:
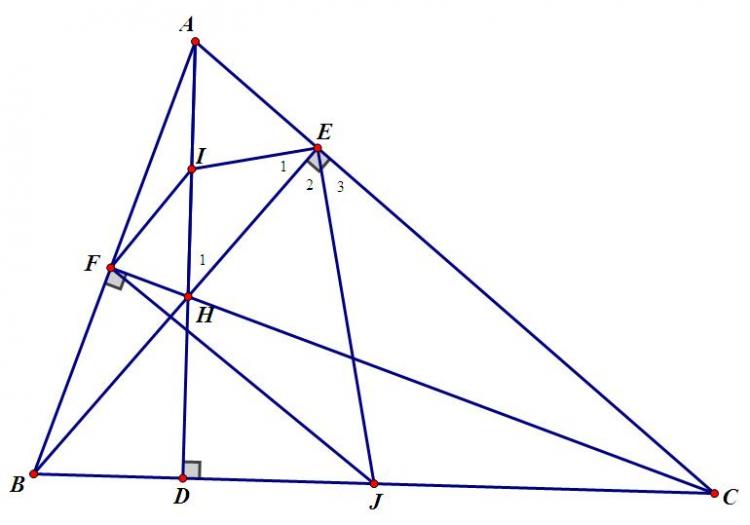
a) Sử dụng tính chất đường trung bình trong tam giác vuông ta có:
(FI = dfrac{1}{2}AH = EI\FJ= dfrac{1}{2}BC = EJ)
Vậy IJ là đường trung trực của EF
b)(widehat E_1=widehat H_1;widehat E_3=widehat {ECJ};widehat H_1=widehat {ECJ} nên widehat H_1=widehat {ECJ})(Cùng phụ góc EAH)
Vậy(widehat E_1=widehat E_3)
(widehat {IEJ}=widehat E_1+widehat E_2=widehat E_3+widehat E_2=90^0)
c)Tứ giác BFHD và ABDE nội tiếp (đpcm)
d) H là giao điểm 3 phân giác của tam giác EFD
Góc PFB = BFD
Góc DFH = EFH
4 góc này cộng lại = 2.90 =180 => P,E,F thẳng hàng
Tương tự ta có F, E, Q thẳng hàng.
Bài tập tự luyện:
Bài 1: Cho tam giác ABCvới trực tâm H. Chứng minh rằng các điểm đối xứng với Hqua các đường thẳng chứa các cạnh hay trung điểm của các cạnh nằm trên đường tròn (ABC).
Bài 2: Cho tam giác ABCvới các đường cao AD, BE, CF. Trực tâm H.DFcắt BHtại M, DEcắt CHtại N. chứng minh đường thẳng đi qua Avà vuông góc với MNđi qua tâm ngoại tiếp của tam giác HBC.
Xem thêm: Cách Tự Đăng Ký Cổng Thanh Toán Trực Tuyến Stripe Là Gì ? Stripe Là Gì
Bài 2:Cho tam giác ABCcó Hlà trực tâm. Plà điểm bất kì trong tam giác đó. Gọi(A_1B_1C_1)là tam giác Pedal của Pvới tam giác ABC. Trên HA, HB, HClấy các điểm(A_2,B_2,C_2)sao cho(AA_2=2PA_1),(BB_2=2PB_1),(CC_2=2PC_1). Chứng minh tam giác ABCđồng dạng với tam giác(A_2B_2C_2).
Xem ngay:Bài 9. Tính chất ba đường cao của tam giác
Hy vọng với những kiến thức tổng hợp trên bạn đã hiểu được khái niệm trực tâm là gì và cách giải các bàitập liên quan. gocnhintangphat.com hy vọng chúng sẽ là những kiến thức hữu ích dành cho bạn. Nếu thấy hay nhớ like và chia sẻ nhé!